Máximos y Mínimos
Entre los valores que puede tener una función (Y) puede haber uno que sea el mas grande y el otro que se el mas pequeño. A estos valores se les llama respectivamente punto máximo y punto mínimo.
Si una función es ascendente es un intervalo y a partir de un punto cualquiera empieza a decrecer, a ese punto se le conoce como punto critico máximo, aunque comúnmente se le llama solo máximo.
Si una función continua es decreciente en cierto intervalo hasta un punto en el cual empieza a ascender, a este punto lo llamamos punto critico mínimo o simplemente mínimo.
Una función puede tener uno, ninguno o varios puntos críticos.
Entre los valores que puede tener una función (Y) puede haber uno que sea el mas grande y el otro que se el mas pequeño. A estos valores se les llama respectivamente punto máximo y punto mínimo.
Si una función es ascendente es un intervalo y a partir de un punto cualquiera empieza a decrecer, a ese punto se le conoce como punto critico máximo, aunque comúnmente se le llama solo máximo.
Si una función continua es decreciente en cierto intervalo hasta un punto en el cual empieza a ascender, a este punto lo llamamos punto critico mínimo o simplemente mínimo.
Una función puede tener uno, ninguno o varios puntos críticos.
Métodos para resolver Máximos y Mínimos
Resolución Método Gráfico (explicación y ejemplo)
Sabemos que:
H=x
V=l.a.h
A= (28-2x)
H= (20-2x)
X Y
0
0
1
507
2
840
3
1023
4
1080
5
1035
6
912
7
735
*Tener f (x) simplificada
V= (28-2x)(21.5-2x)x
V=602x-56x²-43x²+4x³
V= 4x³-99x²+602x
1.-Obtener la derivada dv/dx donde v= volumen x=altura
12x²-198x+602
2.- Igualar la ecuación a cero
3.- Se despeja "X" con la formula general
Donde:
A=
12
B=
-198
C=
602
4.- Sustituir fórmula original con los dos resultados.
V=4x³-99x²+602x
|
V=4x³-99x²+602x
|
V=4(12.42)³-99(12.48)²+602(12.48)
|
V=4(4.01)³-99(4.01)²+602(4.01)
|
V=4(1943.76)-99(155.75)+7512.96
|
V= 4(64.48)-99(16.08)+2414.02
|
V=7775.04-15419.25+7512.96
|
V= 257.92-1591.92+2414.02
|
V= 15288-15419.25
|
V= 2671.94-1591.92
|
V= -131.25
|
V=1080.02
|
Problemario (Solución de problemas de Optimización)
1.-Método de prueba y error
Derivada:
buscar las variaciones de cualquier tipo de función
y
P=200m
2x+2y= 200
2y=200-2x
Y=200-2x/2
Y=100-x
Derivar la
función 100x-x²
Y=100-50
Y=50
100=2x
100/2=x
X=50
2.-Se desea diseñar un tinaco cuya
capacidad sea de 5000 lts. ¿Cuáles deberán de ser las dimensiones de tinaco
para que el material empleado en el mismo sea el mínimo?
1000 lt = m³
1lt = dm³
V= 5m³
V= (Abase)(h)
V= π.x².y
π.x².y= 5
y= 5/ π.x²
M= A base+ A envolvente
M= πx²+2πxy
M= πx²+5πx (5/ πx²)
M= πx²+10/x
1.- Derivar la función
2.- Se iguala a cero y resolver el valor de “x”
X= 1.1675m
ME=
ME=
4.2821m²+8.5650m²
ME= 12.84m²
3.- ¿Cuáles serán las dimensiones de un cilindro si ocupamos también su tapa?
1.
Derivar la función 2πx²+10x-¹
2.- Se iguala a “0” y se resuelve el
valor de “x”
|
ME= 2πx²+2πxy
ME= 2π (.9266m)²+2π(.9266m) (1.8536m)
ME= 5.3946+4.9696m²
ME= 16.1863 m²
5.- ¿Cuál es el diseño óptico de un tinaco para el alimento de los animales de un rancho?
V= 2000lts = 2m³
V= (A base)(h)
V=πx²y/2 semicírculo
V= πx²y/2= 2
V= πx²y=4
Y=4/ πx²
Semi-perímetro
Sp= πd/2
Sp= π2x/2
Sp= πx
M= πx²+ πx(4/ πx²)
M= πx²+ 4/x
2.- igualar a cero
M= πx²+ 4/X
M= π (.8602m)²+4/.8602m
M= 6.9746m²
Granville
1.- Calcular los máximos y mínimos de la función x3_ 6x2+9x
I. 3x2_12x+9
II. 3x2_12x+9=0
III. x2_4x+3=0
(x_1) (x_3)
x_1=0
x=1
x_3=0
x=3
xc1=1
(0)2_4(0)+3=3 +,_
(1.1)2_4(1.1)+3= 1.1_4.4+3= _0.19 Máximo
xc2=3
(2.9)2_4(2.9)+3= 8.41_11.6+3= _0.19 _,+
(3.1)2_4(2.9)+3= 9.61_12.4+3= 0.21 Minimo
(x_1) (x_3)
x_1=0
x=1
x_3=0
x=3
xc1=1
(0)2_4(0)+3=3 +,_
(1.1)2_4(1.1)+3= 1.1_4.4+3= _0.19 Máximo
xc2=3
(2.9)2_4(2.9)+3= 8.41_11.6+3= _0.19 _,+
(3.1)2_4(2.9)+3= 9.61_12.4+3= 0.21 Minimo
IV. x3_6x2+9x
(1)3_6(1)2+9(1)=1_6+9=4
(3)3_6(3)2+9(3)=27_54+27=0
(1)3_6(1)2+9(1)=1_6+9=4
(3)3_6(3)2+9(3)=27_54+27=0
2.- Calcular los máximos y mínimos de la función 2x3+3x2+12x_4
I. 6x2+6x+12
II. 6x2+6x+12=0
III. x2+x+2
(x_1) (x_2)
x_1=0
x=1
x_2=0
x=2
xc1=1
(0)2+0+2=2 +,+
(1.1)2+1.1+2=4.31 No hay maximo ni minimo
xc2=2
(1.9)2+1.9+2=7.51 +,+
(2.1)2+2.1+2=8.51 No hay maximo ni minimo
(x_1) (x_2)
x_1=0
x=1
x_2=0
x=2
xc1=1
(0)2+0+2=2 +,+
(1.1)2+1.1+2=4.31 No hay maximo ni minimo
xc2=2
(1.9)2+1.9+2=7.51 +,+
(2.1)2+2.1+2=8.51 No hay maximo ni minimo
3.- Calcular los máximos y mínimos de la función x3+2x2_15x_20
I. 3x2+4x_15
II. 3x2+4x_15=0
(3x_5) (x+3)
3x_5=0
x=5/3
x+3=0
x=_3
xc1=5/3
3(1)2+4(1)_15= 3+4_15= _8 _,+
3(2)2+4(2)_15= 12+8_15= 5 Mínimo
xc2=_3
3(_4)2+4(_4)_15= 48_16_15= 17 +,_
3(_2)2+4(_2)_15= 12_8_15= _11 Máximo
(3x_5) (x+3)
3x_5=0
x=5/3
x+3=0
x=_3
xc1=5/3
3(1)2+4(1)_15= 3+4_15= _8 _,+
3(2)2+4(2)_15= 12+8_15= 5 Mínimo
xc2=_3
3(_4)2+4(_4)_15= 48_16_15= 17 +,_
3(_2)2+4(_2)_15= 12_8_15= _11 Máximo
III. x3+2x2_15x_20
(5/3)3+2(5/3)_15(5/3)_20= 4.6+3.3_25_20= _37.1
(_3)3+2(_3)_15(_3)_20= _27_6+45_20= _8
(5/3)3+2(5/3)_15(5/3)_20= 4.6+3.3_25_20= _37.1
(_3)3+2(_3)_15(_3)_20= _27_6+45_20= _8
4.- Calcular los máximos y mínimos de la función 2x2_x4
I. 4x_3x3
II. 4x_3x3=0
III.
x_x3=0
x(1_x2)=0
x=0
x=_1
x=1
xc1=0
4(-5)_3(_5)3= (_)
4(5)_3(5)3= (+) Mínimo
xc2=_1
4(_1.5)_3(_1.5)3= _6+10.125= 4.125 +,_
4(_0.5)_3(_0.5)3= _2+0.375= _1.625 Máximo
xc3=1
4(0.5)_3(0.5)3= 2_0.375= 1.625 +,_
4(2)_3(2)3= 8_24= _16 Máximo
x(1_x2)=0
x=0
x=_1
x=1
xc1=0
4(-5)_3(_5)3= (_)
4(5)_3(5)3= (+) Mínimo
xc2=_1
4(_1.5)_3(_1.5)3= _6+10.125= 4.125 +,_
4(_0.5)_3(_0.5)3= _2+0.375= _1.625 Máximo
xc3=1
4(0.5)_3(0.5)3= 2_0.375= 1.625 +,_
4(2)_3(2)3= 8_24= _16 Máximo
5.- Calcular los máximos y mínimos de la función x5_5x4
I. 5x4_20x3
II. 5x4_20x3=0
III. x4_4x3=0
x3(x_4)=0
x1=0
x2=0
x3=0
x4=4
x=0
5(_1)4_20(_1)3= 5+20= 25 +,_
5(1)4_20(1)3= 5_20= _15 Máximo
x=4
5(3)4_20(3)3= 405_540= _135 _,+
5(5)4_20(5)3= 3125_2500= 625 Minimo
x3(x_4)=0
x1=0
x2=0
x3=0
x4=4
x=0
5(_1)4_20(_1)3= 5+20= 25 +,_
5(1)4_20(1)3= 5_20= _15 Máximo
x=4
5(3)4_20(3)3= 405_540= _135 _,+
5(5)4_20(5)3= 3125_2500= 625 Minimo
IV. x5-5x4
(0)5_5(0)4= 0
(4)5_5(4)4= 1024_1280= _256
(0)5_5(0)4= 0
(4)5_5(4)4= 1024_1280= _256
Ejercicios de Maximos y Minimos
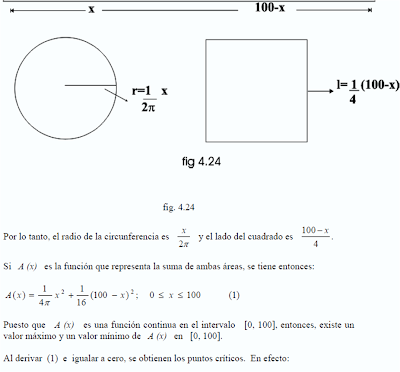
1.- Un alambre de 100 cm. de longitud, se
corta en dos partes formando con una de ellas un círculo y con la otra un
cuadrado. Cómo debe ser cortado el alambre para que:
a. La suma de las áreas de las dos
figuras sea máxima.
b. La suma de las áreas de las dos
figuras sea mínima.
Solución:
Supóngase que el alambre se parte
a una distancia x de uno de sus extremos.
Si x es la longitud de la
circunferencia, entonces 100 – x es el perímetro del cuadrado.
2.- Hallar los
valores máximos y/o mínimos de la función y = x2 − 4x + 7
.
3.- Investigar
los máximos y mínimos de la función y = x3 − 3x2 − 9x + 15
4.- Con
875 metros de rollo de alambrada debe cercarse un terreno rectangular por tres
de sus lados, ya que el cuarto lado estará limitado por el cause de un río. ¿De
qué medidas deberá hacerse para que su superficie sea la máxima abarcada?
5.- Con 875
metros de rollo de alambrada debe cercarse un terreno rectangular por sus
cuatro lados. ¿De qué medidas deberá hacerse para que su superficie sea la
máxima abarcada?
Resolver:
1. f(x) = x3 − 3x + 2
2.- 2x2−3
3.-
x3-3x2-2
4.- f(x)= -8x² –
64x + 3
5.- f(x)=x3-4x2+5x-1
Introducción al Calculo Integral
También llamado anti-derivación. Se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución. Barrow junto con los aportes de Newton, crearon el Teorema fundamental del cálculo integral el cual propone que derivación y la integración son procesos inversos.
Por lo tanto para poder integrar, necesitas conocer primero sobre cálculo diferencial, te recomendamos la siguiente página, ah podrás encontrar fórmulas, procesos, tutoriales, calculadora, entre muchas otras cosas:
https://sites.google.com/site/laskarlas/classroom-news/formulas/calculo-integral
Conoce y aprende más sobre calculo integral en la página siguiente:
http://vamosaintegrar.wordpress.com/
https://sites.google.com/site/laskarlas/classroom-news/formulas/calculo-integral
Conoce y aprende más sobre calculo integral en la página siguiente:
http://vamosaintegrar.wordpress.com/

























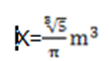





































No hay comentarios:
Publicar un comentario